Las expresiones algebraicas fraccionarias son aquellas en las que las variables están en los denominadores, o forman parte de un numerador con exponente negativo.
Podemos definirlas como el cociente entre dos polinomios P(x)/Q(x), siempre que el divisor no sea el polinomio nulo o el de grado cero.
Las operaciones que se pueden realizar con las expresiones algebraicas no enteras, son la suma, resta, multiplicación y división.
Suma de fracciones con igual denominador
Resta de fracciones con igual denominador
EJEMPLO 2:
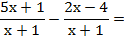
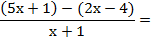
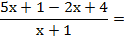
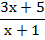
(Con denominadores distintos)
EJEMPLO 3:
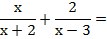
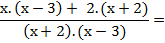
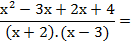
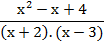
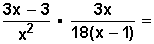
Ejemplo 1 :
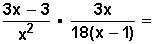
Resolvemos en único paréntesis que tenemos en la expresión:
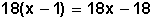
Y la multiplicación nos queda así:
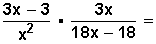
Multiplicamos los numeradores entre sí y los denominadores entres sí
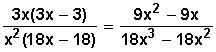
Factorizamos , para poder simplificar hasta donde sea posible:
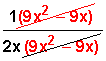
Simpliicamos, eliminando el binomio que se repite en el numerador y el denominador (en rojo), para quedar el resultado
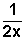
Otra forma sería partiendo por factorizar el primer numerador (3x – 3), para dejar la multiplicación así:
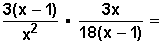
Simplificamos, eliminando el (x – 1) del numerador de la primera fracción y el (x – 1) del denominador de la segunda,
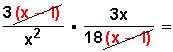
para quedar:
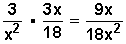
Simplificamos el resultado
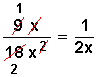
Y obtenemos el mismo resultado.
Este resultado es correcto para cualquier número que sea mayor que 1.
EJEMPLO 1:
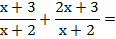
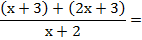
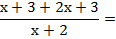
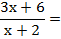
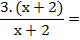
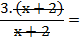 3
3
Las dos fracciones tienen el mismo denominador. El denominador común es ese denominador, y se suman los numeradores; tal como se hace con la suma de fracciones numéricas de igual denominador.
Y si lo piden, aclaremos que la simplificación vale para todo x ≠ -2.
Las dos fracciones tienen el mismo denominador. El denominador común es ese denominador, y se suman los numeradores; tal como se hace con la suma de fracciones numéricas de igual denominador.
Y si lo piden, aclaremos que la simplificación vale para todo x ≠ -2.
EJEMPLO 2:
Las dos fracciones tienen el
mismo denominador. El denominador común es ese denominador, y se suman los
numeradores. Si el segundo numerador tiene más de un término, hay que ponerlo
entre paréntesis para restarlo, ya que es signo menos afectará a todos los
términos.
(Con denominadores distintos)
EJEMPLO 3:
En este ejemplo el
denominador común es el producto de los dos denominadores. Luego se procede
como en la suma de fracciones numéricas: se divide al denominador común por el
denominador de la primera fracción, y al resultado se lo multiplica por el
numerador. Lo mismo con la segunda fracción. Y luego se trabaja en el numerador
para llegar a la mínima expresión.
No siempre el denominador común es el producto de los dos denominadores. En realidad, hay que buscar el mínimo común múltiplo entre ellos.
No siempre el denominador común es el producto de los dos denominadores. En realidad, hay que buscar el mínimo común múltiplo entre ellos.
Multiplicar expresiones algebraicas fraccionarias (racionales)
Entrando en materia, al comienzo hablamos de expresiones algebraicas racionales , que son aquellas en las cuales dos expresiones algebraicas forman una fracción (división, cociente o razón).
Por ejemplo:
Para resolver multiplicaciones con expresiones racionales (que involucren fracciones) debemos tener en cuenta lo siguiente:
- Toda fracción consta de numerador (el número de arriba) y denominador (el número de abajo).
- Para multiplicar fracciones se multiplica numerador por numerador y denominador por denominador.
- Respetar la regla de los signos para la multiplicación.
- Multiplicar entre sí los coeficientes numéricos y entre sí las letras iguales (la parte literal).
- Encontrar o visualizar los factores adecuados para realizar una factorización conveniente, que nos permita luego
- Simplificar o reducir las fracciones a su mínima expresión.
- Reordenar finalmente el numerador y el denominador respetando la secuencia de números y letras (a, b, c, etc.).
Para intentar una mayor comprensión, resolvamos los ejemplos:
Para intentar una mayor comprensión, resolvamos los ejemplos:
Ejemplo 1 :
Resolvemos en único paréntesis que tenemos en la expresión:
Y la multiplicación nos queda así:
Multiplicamos los numeradores entre sí y los denominadores entres sí
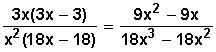
Factorizamos , para poder simplificar hasta donde sea posible:
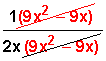
Simpliicamos, eliminando el binomio que se repite en el numerador y el denominador (en rojo), para quedar el resultado
Otra forma sería partiendo por factorizar el primer numerador (3x – 3), para dejar la multiplicación así:
Simplificamos, eliminando el (x – 1) del numerador de la primera fracción y el (x – 1) del denominador de la segunda,
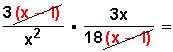
para quedar:
Simplificamos el resultado
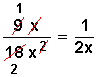
Y obtenemos el mismo resultado.
Este resultado es correcto para cualquier número que sea mayor que 1.
Dividir expresiones algebraicas fraccionarias (racionales)
1) Transformar la división en una multiplicación, invirtiendo la segunda fracción:
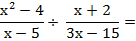
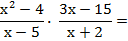
Cambié el signo de división por el de multiplicación, y "dí vuelta" la segunda fracción. Porque, dividir por una fracción, es equivalente a multiplicar por la fracción inversa.
2) Factorizar y reemplazar:
Factorizo todos los polinomios que se puedan factorizar (Hay que saber aplicar los casos de factoreo), y los reemplazo en la fracción que corresponda:
x2 - 4 = con el Quinto Caso de Factoreo (Diferencia de Cuadrados)
x 2
(x + 2).(x - 2)
3x - 15 = con el Primer Caso de Factoreo (Factor Común)
3.(x - 5)
Y luego de factorizar todo lo posible, reemplazo en las fracciones a los polinomios que estaban sin factorizar por sus equivalentes factorizados. Queda así:
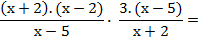
2) Simplificar:
Como ahora la operación es una multiplicación, puedo simplificar como se hace en las multiplicaciones. Aquí, el polinomio (x + 2) está "repetido": aparece en el numerador de la primera fracción, y en el denominador de la segunda. Y el polinomio (x - 5) también está repetido: aparece en el denominador de la primera fracción, y en el numerador de la segunda. Entonces puedo simplificarlos, ya que en la multiplicación de fracciones se simplifica de esa manera: "uno de arriba con uno de abajo".
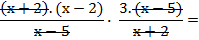
1 1
En los denominadores de ambas fracciones se me hace necesario poner el "1" que queda cuando se simplifica, porque no quedó nada más en los denominadores de esas fracciones, y algo hay que poner para saber luego qué es lo que estamos multiplicando.
Y si lo piden, aclaremos para qué valores de x vale esa simplificación:
x + 2 ≠ 0
x ≠ -2
x - 5 ≠ 0
x ≠ 5
3) Multiplicar:
Luego de simplificar, las dos fracciones ("pasadas en limpio") quedaron así:
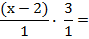 (Este paso no es necesario, se puede obviar)
(Este paso no es necesario, se puede obviar)
Ahora multiplico lo que quedó: "lo de arriba con lo de arriba y lo de abajo con lo de abajo". El resultado es una fracción formada por ambos resultados:
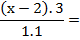 (Este paso tampoco es imprescindible)
(Este paso tampoco es imprescindible)
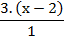 = (Queda mejor con el "3" adelante) (Otro paso que se puede obviar)
= (Queda mejor con el "3" adelante) (Otro paso que se puede obviar)
3.(x - 2)
Cambié el signo de división por el de multiplicación, y "dí vuelta" la segunda fracción. Porque, dividir por una fracción, es equivalente a multiplicar por la fracción inversa.
2) Factorizar y reemplazar:
Factorizo todos los polinomios que se puedan factorizar (Hay que saber aplicar los casos de factoreo), y los reemplazo en la fracción que corresponda:
x2 - 4 = con el Quinto Caso de Factoreo (Diferencia de Cuadrados)
x 2
(x + 2).(x - 2)
3x - 15 = con el Primer Caso de Factoreo (Factor Común)
3.(x - 5)
Y luego de factorizar todo lo posible, reemplazo en las fracciones a los polinomios que estaban sin factorizar por sus equivalentes factorizados. Queda así:
2) Simplificar:
Como ahora la operación es una multiplicación, puedo simplificar como se hace en las multiplicaciones. Aquí, el polinomio (x + 2) está "repetido": aparece en el numerador de la primera fracción, y en el denominador de la segunda. Y el polinomio (x - 5) también está repetido: aparece en el denominador de la primera fracción, y en el numerador de la segunda. Entonces puedo simplificarlos, ya que en la multiplicación de fracciones se simplifica de esa manera: "uno de arriba con uno de abajo".
1 1
En los denominadores de ambas fracciones se me hace necesario poner el "1" que queda cuando se simplifica, porque no quedó nada más en los denominadores de esas fracciones, y algo hay que poner para saber luego qué es lo que estamos multiplicando.
Y si lo piden, aclaremos para qué valores de x vale esa simplificación:
x + 2 ≠ 0
x ≠ -2
x - 5 ≠ 0
x ≠ 5
3) Multiplicar:
Luego de simplificar, las dos fracciones ("pasadas en limpio") quedaron así:
Ahora multiplico lo que quedó: "lo de arriba con lo de arriba y lo de abajo con lo de abajo". El resultado es una fracción formada por ambos resultados:
3.(x - 2)
No hay comentarios.:
Publicar un comentario