Usamos desigualdades cuando existe un rango de posibles soluciones para una situación. "Debo estar ahí en menos de 5 minutos," "Este equipo necesita meter por lo menos un gol para poder ganar," y "Para ir y venir de la ciudad, necesito por lo menos $6.50 para pagar el tren" son todos ejemplos de situaciones donde un límite es especificado, pero un rango de posibilidades existe más allá de ese límite. Eso es en lo que estamos interesados cuando estudiamos desigualdades — posibilidades.
Podemos explorar las posibilidades de una desigualdad usando la recta numérica. Esto es suficiente para situaciones simples, como la desigualdades de una sola variable. Pero en circunstancias más complicadas, como aquellas de dos variables, es más útil añadir otra dimensión, y usamos un eje de coordenadas. En estos casos, usamos desigualdades lineales — desigualdades que pueden escribirse con la forma de una ecuación lineal.
Desigualdades de Una Variable
Las desigualdades con una variable pueden ser graficadas en la recta numérica, como es el caso de la desigualdad x ≥ -2:
Aquí hay otra representación de la misma desigualdad x ≥ -2, esta vez graficada en un eje de coordenadas:
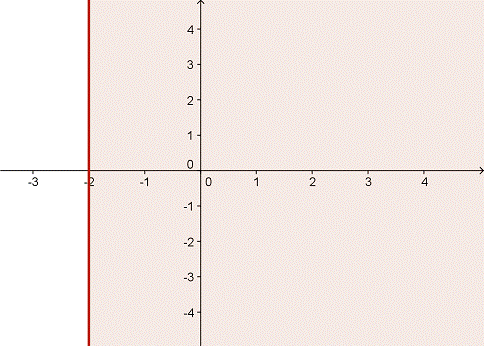
En esta gráfica, primero trazamos la recta x = -2, y luego sombreamos toda la región del lado derecho de la recta. El área sombreada se llama región limitada, y cualquier punto dentro de esta región satisface la desigualdad x ≥ -2. Nota también que la línea representando el límite de la región es una línea sólida; esto quiere decir que los valores sobre la recta x = -2 están incluidos en el conjunto de soluciones de la desigualdad.
Como contraste, veamos la siguiente gráfica, la cual muestra y < 3:
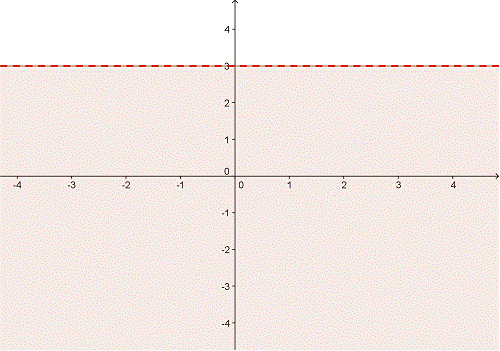
En esta desigualdad, la línea límite se grafica como una línea punteada. Esto significa que los valores sobre la recta no están incluidos en el conjunto de soluciones de la desigualdad.
Nota que en los dos ejemplos utilizamos las variables x y y. Es práctica estándar usar estas variables cuando estas graficando una desigualdad en un eje de coordenadas (x, y).
Desigualdades de Dos Variables
Las graficas de x ≥ -2 y y < 3, mostradas arriba no tienen nada de especial. Pudimos haber representado las dos relaciones en una recta numérica, y dependiendo del problema que tratamos de resolver, habría sido más fácil hacerlo.
Las cosas se vuelven más interesantes cuando graficamos desigualdades lineales con dos variables. Empecemos con una desigualdad básica de dos variables: x > y.
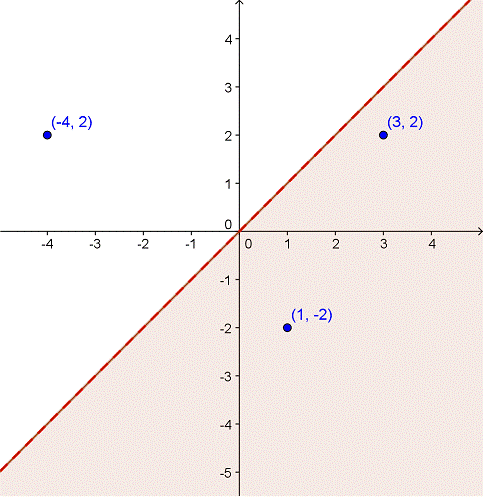
La línea límite está representada por una línea punteada sobre x = y. Todos los puntos bajo la línea están sombreados; este es el rango de puntos donde la desigualdad x > y es válida. Observa los tres puntos que han sido identificados en la gráfica. ¿Ves que los puntos en la región límite tienen valores x mayores que los valores y, mientras que el punto fuera de la región no?
Graficar otras desigualdades en la forma estándar y = mx + b es bastante simple también. Una vez que graficamos la línea límite, podemos encontrar cuál es la región a sombrear si probamos algunos pares ordenados dentro de la región o, en muchos casos, sólo observando la desigualdad.
La gráfica de la desigualdad y > 4x − 5.5 se muestra abajo. La línea límite es la recta y = 4x − 5.5, y está punteada porque nuestro término y es “mayor que,” no “mayor o igual que.”
Para identificar la región límite, la región donde la desigualdad es verdadera, podemos probar algunos pares de coordenadas, uno en cada lado de la línea límite.
Si sustituimos (-1, 3) en y > 4x − 5.5, encontramos 3 > 4(-1) − 5.5, o 3 > -9.5. Esto es una declaración válida. Parece que debemos sombrear el área hacia la izquierda de la recta.
Por otro lado, si usamos (2, -2) en y > 4x − 5.5, encontramos -2 > 4(2) − 5.5, o -2 > 2.5. Esto no es una declaración válida, por lo que el punto (2, -2) no está dentro del conjunto solución. Si, la región límite está a la izquierda de la línea límite.
Desigualdades en Contexto
Entender la importancia de la región sombreada en una desigualdad puede ser un poco difícil sin asignarle un contexto. El siguiente problema muestra un ejemplo donde la región sombreada nos ayuda a entender el rango de posibilidades.
Celia y Juniper quieren donar dinero a un banco de alimentos local. Para recaudar fondos, ellas venden collares y aretes que han fabricado ellas mismas. Los collares cuestan $8 y los aretes $5. ¿Cuál es el rango de posibles ventas que pueden hacer para donar por lo menos $100?
El primer paso aquí es crear la desigualdad. Una vez que la tengamos, podemos resolverla y crear su gráfica para entender mejor la importancia de la región límite. Empecemos con asignar la variable x al número de collares vendidos y y al número de aretes vendidos. (Recuerda — como vamos a graficar en un eje de coordenadas, debemos usar las variables x y y.)
cantidad de dinero ganado por la venta de collares
|
+
|
cantidad de dinero ganado por la venta de aretes
|
≥
|
$100
|
8x
|
+
|
5y
|
≥
|
100
|
Podemos manipular esta desigualdad para resolver y. Esta es la forma pendiente-intersección, y hará que la línea límite sea más fácil de graficar.
Ejemplo
| |||||
Problema
|
8x
|
+
|
5y
|
≥
|
100
|
8x − 8x
|
+
|
5y
|
≥
|
100 − 8x
| |
5y
|
≥
|
100 − 8x
| |||
 |
≥
|  | |||
y
|
≥
|
20 −
 | |||
Solución
|
y
|
≥
|
−
+ 20 | ||
La forma pendiente-intersección de la desigualdad es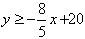 
. Tracemos la gráfica:
. Tracemos la gráfica:
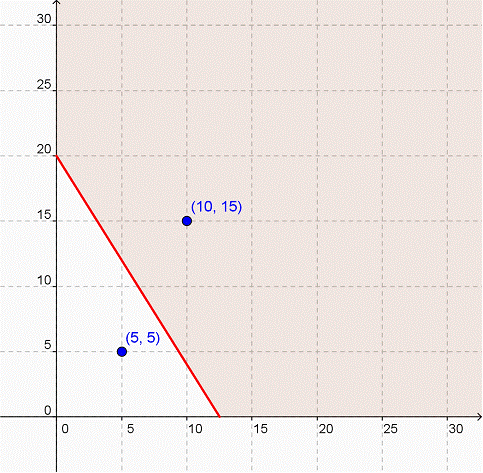
La región sombreada representa todas las posibles combinaciones de collares y aretes que Celia y Juniper podrían vender para juntar por lo menos $100 para el banco de alimentos. ¡Es un rango bastante amplio!
Podemos usar los dos pares ordenados para confirmar que hemos sombreado la región correcta. Si sustituimos (10, 15) en la desigualdad, encontramos 8(10) + 5(15) ≥ 100, la cual es una declaración válida. Sin embargo, si usamos (5, 5) creamos una declaración inválida: 8(5) + 5(5) es sólo 65, y es menor que 100.
Nota que mientras que todos los puntos satisfacen la desigualdad, no todos los puntos tendrán sentido en este contexto. Por ejemplo (21.25, 10.5). Si bien cae dentro de la región sombreada, ¡es difícil imaginar que puedan vender 21.25 collares y 10.5 aretes! Celia y Juniper pueden ver muchas posibles combinaciones en la región límite para planear cuántas joyas fabricar.
Intervalo
Un subconjunto de la recta real se llama intervalo, y contiene a todos los números reales que están comprendidos entre dos cualesquiera de sus elementos.
Geométricamente los intervalos corresponden a segmentos de recta, semirrectas o la misma recta real.
Los intervalos de números correspondientes a segmentos de recta son intervalos finitos, los intervalos correspondientes a semirrectas y a la recta real son intervalos infinitos.
Los intervalos finitos pueden ser cerrados, abiertos o semiabiertos.
Sean a y b dos números reales tales que a < b.
Intervalo cerrado
Es el conjunto de números reales formado por a, b y todos los comprendidos entre ambos.
[a, b] = { x / a £ x £ b}
Intervalo abierto
Es el conjunto de los números reales comprendidos entre a y b.
(a, b) = {x / a < x < b}
Intervalo semiabierto a izquierda (o semicerrado a derecha)
Es el conjunto de números reales formado por b y los números comprendidos entre a y b.
(a, b] = {x / a < x £ b}
Es el conjunto de números reales formado por a y los números comprendidos entre a y b.
[a, b) = { x / a £ x < b}
Intervalos infinitos
[a, +¥) = { x / x ³ a} (a, +¥) = { x / x > a}
(-¥ , b] = { x / x £ b} (-¥ , b) = { x / x < b}
(-¥ , +¥ ) = R
Ejemplo. Interprete gráficamente los intervalos: a) [-2, 3] b) (1, 4) c) (0, 5] d) [1, +¥ ) e) (-¥ , 3)
a) El intervalo [-2, 3] comprende todos los números reales entre -2 y 3. Como es cerrado incluye los extremos. Su representación gráfica es:
b) El intervalo (1, 4) corresponde a todos los números reales entre 1 y 4. Es abierto pues no incluye a los extremos. Gráficamente:
c) El intervalo (0, 5] comprende todos los números reales entre 0 y 5 incluyendo el extremo 5. Se trata de un intervalo semiabierto a izquierda o bien semicerrado a derecha. Su gráfica es:
d) El intervalo [1, +¥ ) es infinito y comprende todos los números reales mayores o iguales a 1. Gráficamente:
e) El intervalo (-¥, 3) es infinito y comprende todos los números reales menores que 3. Su gráfica es:
A modo de resumen:
| Nombre del intervalo | Notación conjuntista | Notación de intervalos | Representación gráfica |
| Abierto | {x / a < x < b} | (a, b) |  |
| Semicerrado a derecha | {x / a < x £ b} | (a, b] |  |
| Semicerrado a izquierda | { x / a £ x < b} | [a, b) |  |
| Cerrado |
{ x / a £ x £ b}
| [a, b] |  |
| Infinito abierto a izquierda | { x / x > a} | (a, +¥ ) |  |
| Infinito cerrado a izquierda | { x / x ³ a} | [a, +¥ ) |  |
| Infinito abierto a derecha | { x / x < b} | (-¥ , b) |  |
Infinito cerrado a derecha
| { x / x £ b} | (-¥ , b] |  |
| Infinito | R | (-¥ , +¥ ) |  |
En Conclusión:
Las desigualdades pueden ser graficadas en una recta numérica o en un eje de coordenadas. Cuando usamos el eje de coordenadas, el rango de posibles soluciones está representado como un área sombreada en el plano. La línea límite de la desigualdad es trazada como una línea sólida si los puntos en ella satisfacen la desigualdad, como en los casos ≤ y ≥. Es dibujada como una línea punteada si los puntos sobre ella no satisfacen la desigualdad, como en los casos de < y >. Usar un eje de coordenadas es especialmente útil para entender el rango de soluciones posibles para desigualdades con dos variables.
No hay comentarios.:
Publicar un comentario