Números Reales

Numero Reales 

El conjunto de los números reales pertenece en matemáticas a la recta numérica que comprende a los números racionales y a los números irracionales. Esto quiere decir que incluyen a todos los números positivos y negativos, el símbolo cero, y a los números que no pueden ser expresados mediante fracciones de dos enteros que tengan como denominador a números no nulos (excluye al denominador cero).

Un número real puede ser expresado de diferentes maneras, por un lado están los números reales que pueden ser expresados con mucha facilidad, ya que no poseen reglas complejas para hacerlo. Estos son los números enteros y los fraccionarios, como por ejemplo el número $67$ que viene a ser un entero, o también el $\frac{3}{4}$, que es un número fraccionario compuesto de dos enteros, cuyo numerador es $3$ y su denominador es $4$. Sin embargo, también existen otros números que pueden ser expresados bajo diferentes reglas matemáticas más complejas como números cuyos decimales son infinitos como el número $\pi$ o $\sqrt{2}$ y que sirven para realizar cálculos matemáticos pero no pueden ser representados como un símbolo numérico único

Los números reales se representa con la letra $R$, y aparecen por la necesidad de realizar cálculos más complejos ya que en épocas como entre el siglo XVI y el XVII, se hacían necesarias nuevas cifras para los avances tecnológicos que ya no podían ser representados por cifras aproximadas ni por expresiones coloquiales por su inexactitud. El rigor del avance de la humanidad a partir de sus herramientas, hizo necesaria la creación de nuevas expresiones matemáticas que den mayor exactitud a los cálculos

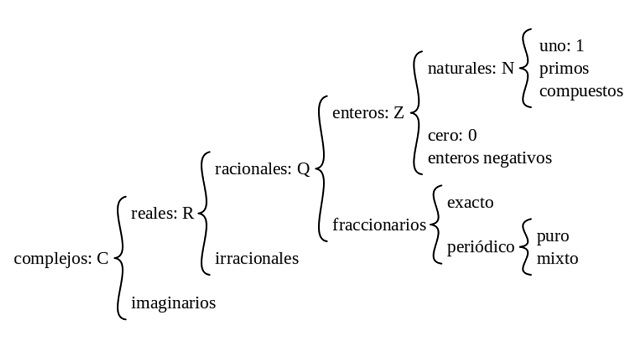
CLASIFICACIÓN DE LOS NÚMEROS (TIPOS)

• Los Números Naturales «N» son todos los números mayores de cero* (algunos autores incluyen también el 0) que sirven para contar. No pueden tener parte decimal, fraccionaria, ni imaginaria. N= [1, 2 , 3, 4, 5…]

• Los Números Enteros «Z» incluye al conjunto de los números naturales, al cero* y a sus opuestos (los números negativos). Es decir: Z = […-2, -1, 0, 1, 2…]

• Los Números Racionales «Q» son aquellos que pueden expresarse como una fracción de dos números enteros. Por ejemplo: Q = [¼, ¾, etc.]

• Los Números Reales «R» se definen como todos los números que pueden expresarse en una línea continua, por tanto incluye a los conjuntos anteriores y además a los números irracionales como el número «∏» y «e».

• Los Números Complejos «C» incluye todos los números anteriores más el número imaginario«i». C = [N, Z, Q, R, I].